One of the things I like about retrocomputing is the way the limitations of older computers give a "grain" to the software that runs on them, like how film grain affects the quality of the image in a movie. The color-fringed text of an Apple ][, the distinct color palettes of the Commodore 64 or NES, the slightly elongated rectangular pixels of DOS graphics, or the stark black-and-white and idiosyncratic dithering algorithms of the Macintosh all make it so you can immediately tell a screenshot from any of these old systems.
Now that our computers can render almost anything in any style in real time, I like to imagine what other "grains" a fantasy console could impose, for purely stylistic reasons instead of hardware limitations. What if, instead of square or rectangular pixels, everything had to be composed out of pattern blocks, or tangrams, or some other tiling system? This could give the same sort of chunky, discrete feel as pixel art, but with just a bit more flexibility: traditional pixel art can only rotate in multiples of 90º without having to be resampled, but pattern blocks can rotate in 30º intervals while staying "on the grid".

Although we could easily implement such a system by building shapes out of triangles with floating-point coordinates, that wouldn't be any fun—we'd have to manage accumulating error from floating-point math, and it'd also be possible to cheat the system by including coordinates that don't strictly fit the grain we're trying to impose. Pixel art forces every pixel to be at a pair of integer coordinates on a strict grid, but what does that "grid" look like for different tiling systems? Let's talk about it.
Finding the minimum number of axes needed
The nice thing about a rectangular grid is that we only need two integer coordinates to address any point on the grid, the familiar Cartesian x and y. It isn't hard to see why only two coordinates are necessary. Starting from an origin point, any other point on the grid can be reached by some combination of steps in one of the four possible directions:
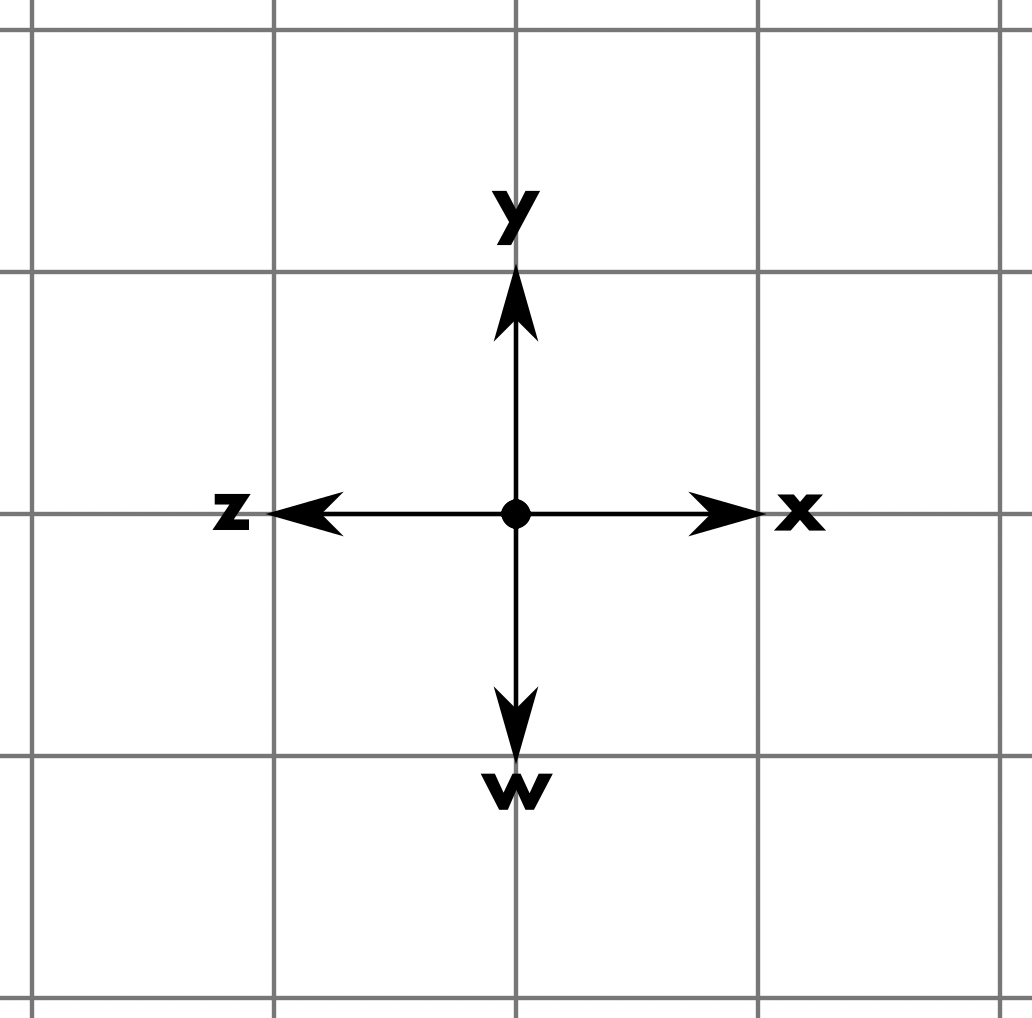
Two of these are clearly opposites of the other two: if you go x then z, you're right back where you started, same as if you go y then w. And if you go xxxzz, the two zs just cancel out two of the xs and you end up in the same position as if you'd taken one x step. Also, taking the same collection of steps in any order puts you at the same point in the grid; in other words, xyyx gets you to the same place as xxyy. So to address any point in the grid, we only need to know how many x steps and how many y steps it takes to get there, and we can use negative integers for x and/or y to represent the opposite z and w directions.
Let's try something similar for pattern block tilings. From any point on the grid, we can go in one of twelve directions, at any multiple of 30º:
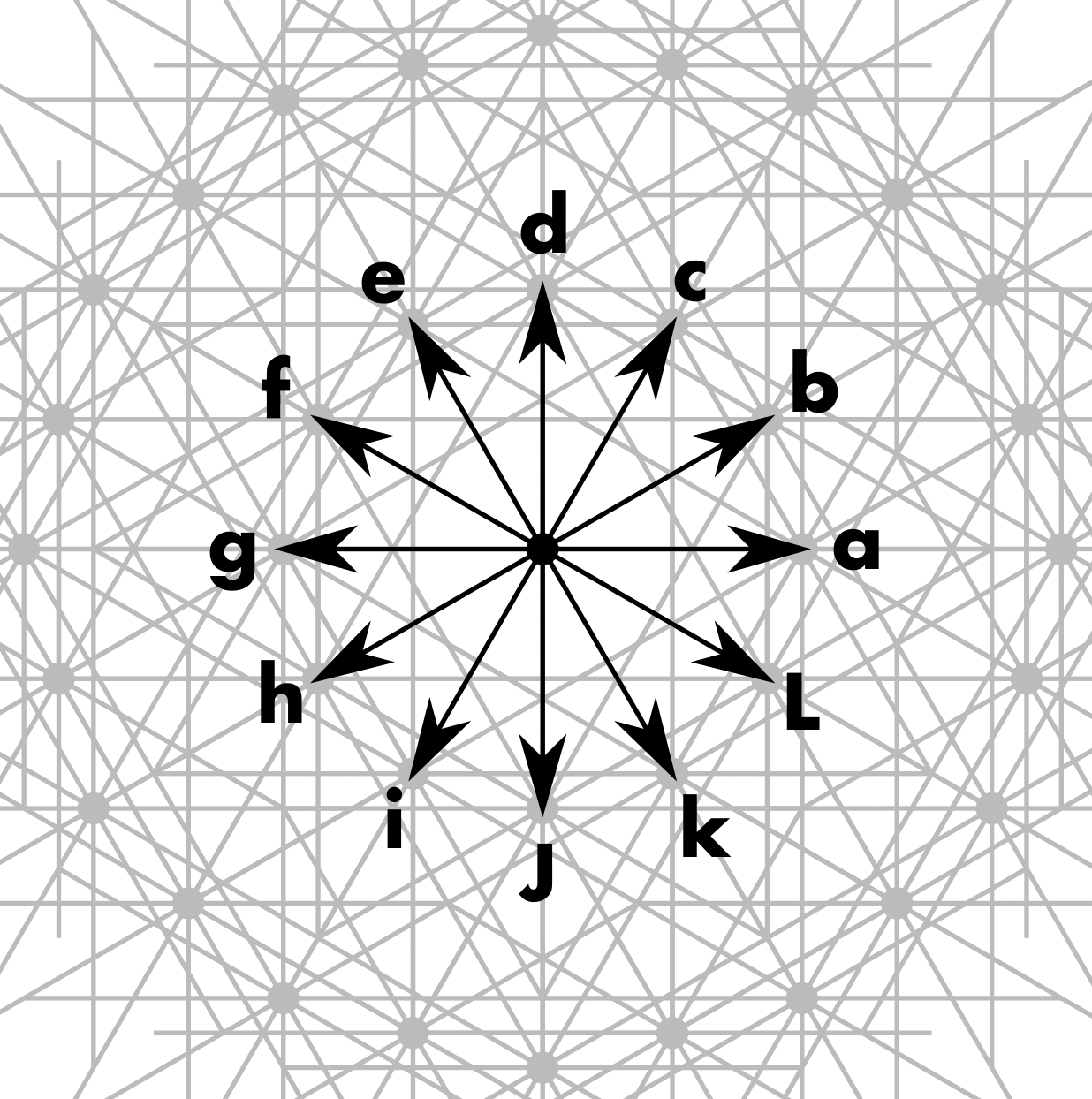
This is much less neat of a "grid", since unlike the Cartesian grid, the directions don't all fit together neatly—if you take one b step followed by one L step, then you end up on a point that's parallel to a, but between a and 2a, and there are in fact infinitely many such points we can reach (but only countably infinite, not a continuum). Nonetheless, combining steps in these 12 directions will get us anywhere we could get following the edges of some combination of pattern blocks. If we don't absolutely have to, though, we don't want to have to store twelve coordinates for every point. Just like with the Cartesian grid, we can quickly knock out six of these axes as redundant because they're negations of the other six, but six coordinates is still a lot—can we do even better?
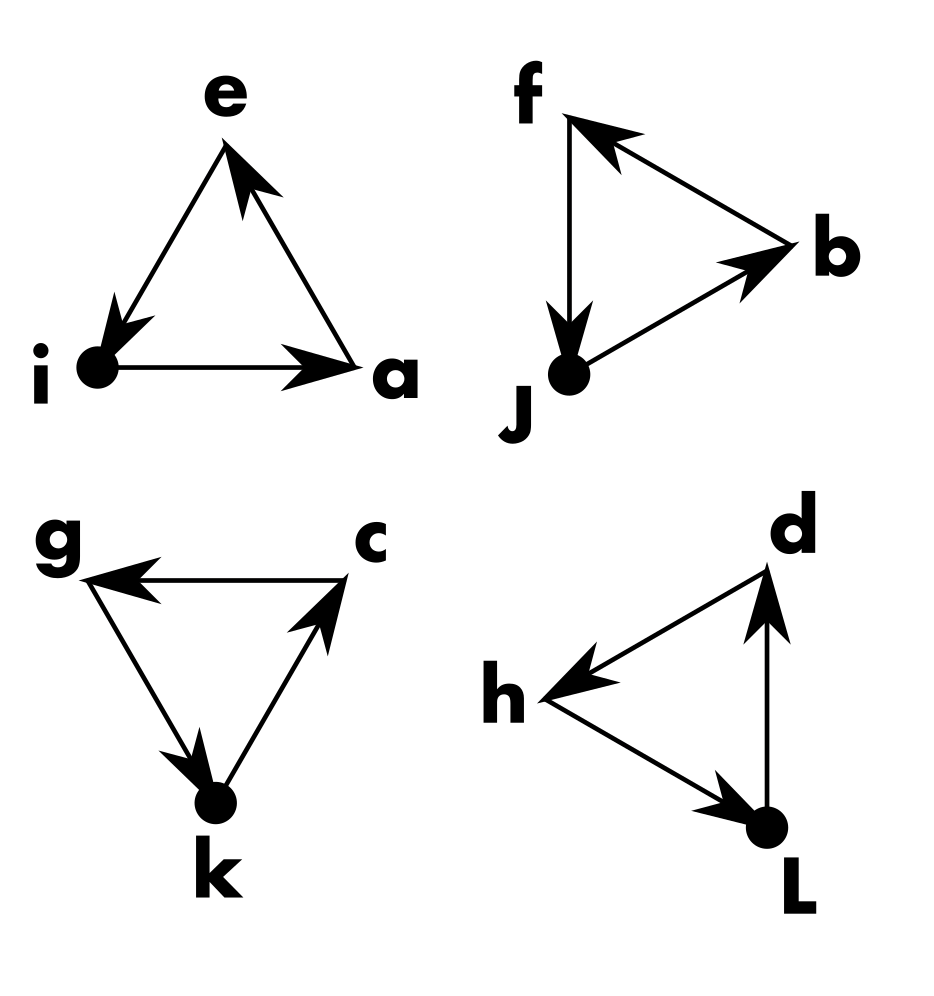
With twelve directions to choose from, in addition to going forward and backward in opposing directions, we can also form equilateral triangles by taking steps in three directions at 60º angles to each other, which suggests another redundancy among the twelve coordinates: doing a little algebra, since a + e + i = 0, and we already know that i is -c, that means e = -a + c. Along the same lines, b + f + j = 0 too, and j is -d, so f = -b + d. So that's two more axes we don't need, leaving us with only four. We already know g is -a, so c + g + k = 0 means c - a - e = 0, but we already know e = -a + c, so there aren't any further axes we can knock out this way. Four ends up being the minimum number of axes we need to address any point on the corners of a pattern block arrangement.
We can also trace out squares using combinations of the twelve directions, like a + d + g + j = 0, and regular hexagons like b + d + f + h + j + l = 0, as well as the regular dodecagon a + b + c + d + e + f + g + h + i + j + k + l = 0, but these equations don't end up teaching us anything new about the relationships among the directions, since they're really just combinations of the equations we got from the looking at the opposite pairs or the equilateral triangles—we already know a + g = 0 and d + j = 0, so a + d + g + j = 0 isn't new information; likewise, we already saw that b + f + j = 0 and d + h + l = 0, so the regular hexagon relation b + d + f + h + j + l = 0 doesn't help.
To generalize, it turns out that for a tiling system that allows for travel in n evenly-angled directions, then only the prime factors of n fundamentally create redundancies among the directions—we saw that in the case of 12 directions from the opposite pairs (factor 2) and the equilateral triangles (factor 3). The minimum number of axes to represent all n directions ends up being the totient of n, that is, the count of positive integers less than n that don't share any prime factors with n. Looking back at the Cartesian grid, with four evenly-spaced directions, we need two axes, which matches the totient of 4 being 2 (since 1 and 3 both have no common prime factors with 4). Board game nerds know that you can also tile the plane with regular hexagons, and a hexagonal grid offers 6 directions to go from any space to its neighboring spaces, and the totient of 6 also happens to be 2 (thanks to 1 and 5 not sharing prime factors with 6), so you can also represent positions on a hex grid with only two axes. With the four axes we're using for the pattern block coordinate system, we could instead represent a system for tangrams, which have 45º angles, or eight directions to choose from, or for Penrose tilings, which traditionally use multiples of 36º angles, or ten directions to choose from, since the totient of both 8 and 10 is also four. If you wanted a coordinate system that can represent all 360 degrees, then you'd need 96 axes, since the totient of 360 is 96.
Rotation and flipping
Getting back to the 12-direction pattern block coordinate system, we can represent any position as four coordinates n₀*a + n₁*b + n₂*c + n₃*d. To rotate counterclockwise 30º, we move all those coordinates over one axis to give n₀*b + n₁*c + n₂*d + n₃*e. Since e = -a + c, that becomes -n₃*a + n₀*b + (n₁ + n₃)*c + n₂*d. We can apply this transformation repeatedly to see that it iterates through all of the directions:
rotate (n0, n1, n2, n3) = (-n3, n0, n1 + n3, n2)
rotate ( 1, 0, 0, 0) -- ( 0, 1, 0, 0), b
rotate ( 0, 1, 0, 0) -- ( 0, 0, 1, 0), c
rotate ( 0, 0, 1, 0) -- ( 0, 0, 0, 1), d
rotate ( 0, 0, 0, 1) -- (-1, 0, 1, 0), e
rotate (-1, 0, 1, 0) -- ( 0, -1, 0, 1), f
rotate ( 0, -1, 0, 1) -- (-1, 0, 0, 0), g
We can similarly do horizontal and vertical flips by flipping the individual axes, so vertically flipping n₀*a + n₁*b + n₂*c + n₃*d gives n₀*a + n₁*l + n₂*k + n₃*j, which reduces down to n₀*a - n₁*f - n₂*e - n₃*d, then n₀*a - n₁*(-b + d) - n₂*(-a + c) - n₃*d, giving (n₀ + n₂)*a + n₁*b - n₂*c + (-n₁ - n₃)*d.
vflip (n0, n1, n2, n3) = (n0 + n2, n1, -n2, -n1 - n3)
vflip ( 1, 0, 0, 0) -- ( 1, 0, 0, 0)
vflip ( 0, 1, 0, 0) -- ( 0, 1, 0, -1), l
vflip ( 0, 0, 1, 0) -- ( 1, 0, -1, 0), k
vflip ( 0, 0, 0, 1) -- ( 0, 0, 0, -1), j
vflip ( 0, 1, 0, -1) -- ( 0, 1, 0, 0), b
If you've ever done 3D graphics, then you've probably used matrices to represent transformations, and we can do the same thing here. Matrices can represent not only individual transforms, but can compose multiple transforms by multiplying matrices together, and we can do the same thing by representing these pattern tile transformations as matrices. The 30º rotation transform can be written as a matrix like:
R = ⎡ 0 0 0 -1⎤
⎢ 1 0 0 0⎥
⎢ 0 1 0 1⎥
⎣ 0 0 1 0⎦
and matrices for 60º, 90º, 120º, etc. rotation can be formed by multiplying the matrix by itself repeatedly. Similarly, we could construct matrices for flipping by one axis, and derive flips around the other axes by combining rotation and flipping matrices.
Distance and length
To do things like determine the distance between objects, detect collisions, and so on, we could convert to floating-point Cartesian coordinates and use off-the-shelf algorithms, but for fun, let's see how far we can get staying in the discrete coordinate system we've set up. In Cartesian coordinates, the Pythagorean theorem turns an xy coordinate pair into the distance from the origin to the point addressed by those coordinates, since the distances along the x and y coordinates always form a right triangle along with the distance we're measuring. In our pattern block coordinate system, though, there are four coordinates to consider, forming a pentagon along with the distance to measure. Thankfully, the Pythagorean theorem generalizes to the law of cosines, and we can directly compute the distance from the origin to a point using:
distance (a, b, c, d) = sqrt (a*a + b*b + c*c + d*d
- 2*((a*b + b*c + c*d) * cos 150º
+ (a*c + b*d) * cos 120º
+ (a*d) * cos 90º))
which, since cos 150º = -cos 30º = sqrt(3)/2, cos 120º = -cos 60º = 1/2, and cos 90º = 0, simplifies to:
distance (a, b, c, d) = sqrt (a*a + b*b + c*c + d*d
+ sqrt(3) * (a*b + b*c + c*d)
+ a*c + b*d)
Instead of computing this as a floating-point value, we can keep the distance value discrete by representing it as the pair of integers n and m that plug into the equation √(n + m*√3) that every possible distance in this coordinate system must fit into.
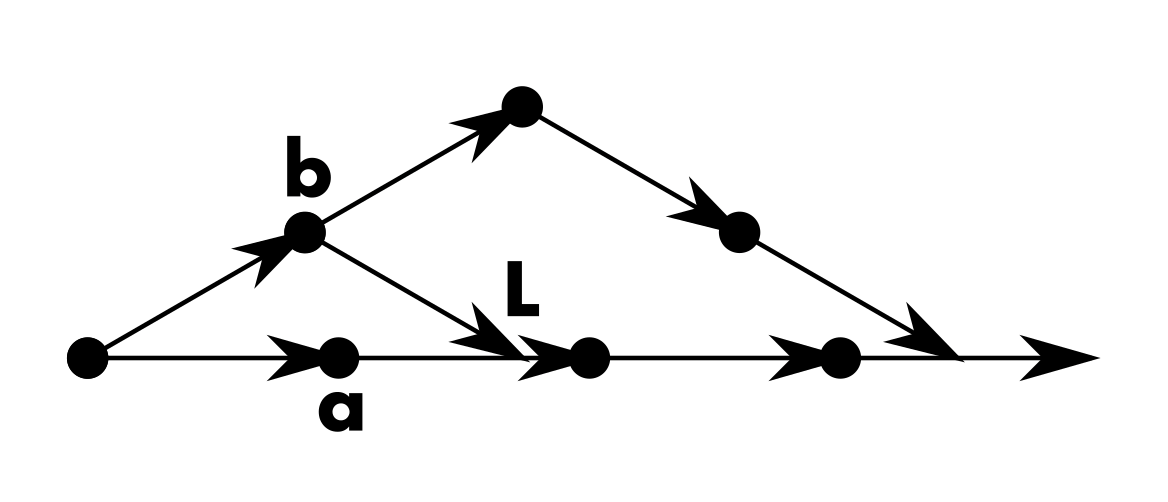
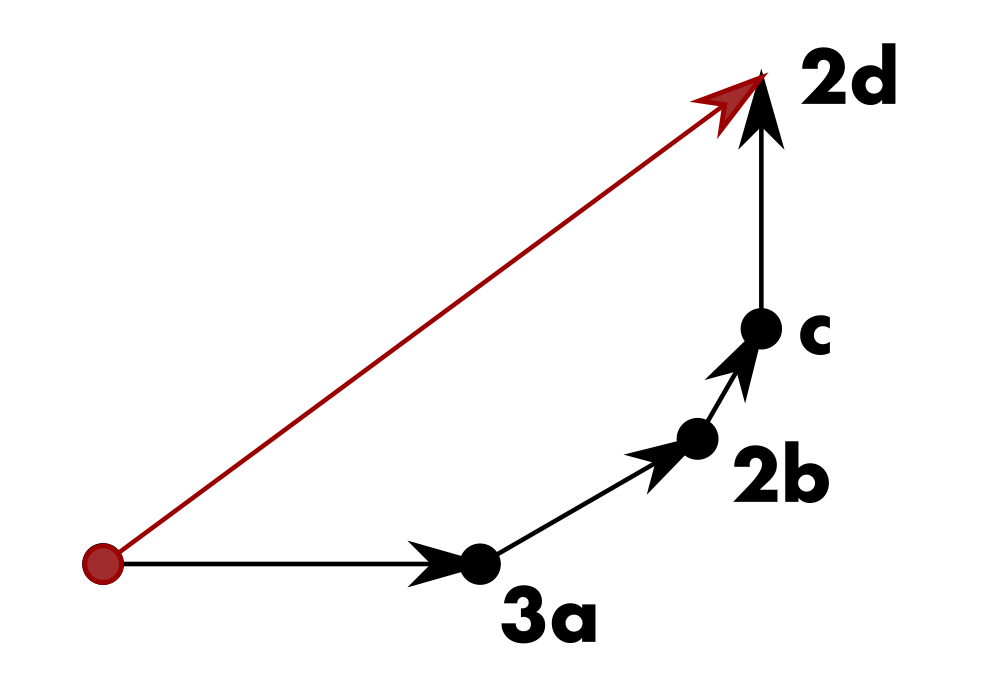
One interesting thing about the pattern block coordinate system is that, despite being made of discrete integer coordinates, we can still represent non-integer points between the integer increments by combining the other axes. For instance, we can travel horizontally in integer increments along the a direction; however, if we take one step in the b direction followed by another step in the complementary l direction, then we also end up traveling a net horizontal distance, but at a point between one a and 2a. This point happens to be 2 * cos 30º, or √3. We can take any number of steps n in the b direction, followed by the same number of steps in the l direction, and end up at a point n√3 units away from the origin. By combining integer and √3 steps, we can end up at any point m + n√3 on the horizontal axis, or any of the other axes for that matter. Remember how rational fractions can get arbitrarily close to, but never exactly reach, irrational numbers like square roots? We have an interesting opposite situation here—we could get arbitrarily close to a fractional point on the axis, such as 1/2 of the way, by picking large values of m and n such that m + n√3 gets closer and closer to 1/2, but we still can't precisely reach that point.
That's all for now
I could write a lot more, but this post is already getting long, and now that work's back I want to post what I've got in case I never get back to continuing this. I find these coordinate systems interesting to think about, and it'd be fun to build a game or art program around them someday. Although I mostly talked about pattern blocks and 12-direction coordinate systems, the coordinate systems you get from splitting in a different number of directions all have their own different unique properties; a 10-direction system is particularly interesting, because it gives you easy access to golden ratio relationships, and it also forbids right angles, so as a "grain" for a game art style it could encourage some interesting organic design patterns.