How to write your next math function in the style of John Carmack: understanding the "fast" inverse square root

October 16, 2022

One of the more infamous bits of code associated with John Carmack (albeit not invented by him) is the "fast" inverse square root function from Quake III, which computes $\frac{1}{\sqrt{x}}$ in an unconventional way that was faster than floating-point division and square root on old CPUs:

float Q_rsqrt( float number )
{
	long i;
	float x2, y;
	const float threehalfs = 1.5F;

	x2 = number * 0.5F;
	y  = number;
	i  = * ( long * ) &y;                       // evil floating point bit level hacking
	i  = 0x5f3759df - ( i >> 1 );               // what the fuck? 
	y  = * ( float * ) &i;
	y  = y * ( threehalfs - ( x2 * y * y ) );   // 1st iteration
//	y  = y * ( threehalfs - ( x2 * y * y ) );   // 2nd iteration, this can be removed

	return y;
}

This bit of code is often held up as an artifact of inscrutable genius, incomprehensible to the feeble minds of us sub-Carmack intelligences, but if you can handle high school math, you can understand this function, and you can even use the same technique to write your own "fast" functions in a similar style. Let's walk through how this function works, refactor it to be less mystifying, and then reuse its techniques to implement another "fast" math function in the same style.

Logarithms and floating-point representation

In case you forgot, a logarithm function is the inverse of exponentiation. If $2^{8} = 256$ , then the base-two logarithm of 256 is 8, written $\log_{2} 256 = 8$ . We like logarithms in algorithmic complexity theory because O(log n) algorithms scale well—the relative cost of increasing the size of their workload gets smaller as the workload gets larger—but another useful property of logarithms is that we can compute multiplication, division, roots, and exponents of numbers using cheaper addition, subtraction, division, and multiplication operations on their logarithms:

If…	…then…
$a b = c$	$\log a + \log b = \log c$
$\frac{a}{b} = c$	$\log a - \log b = \log c$
$a^{n} = c$	$n \log a = \log c$
$\sqrt[n]{a} = c$	$\frac{\log a}{n} = \log c$

To compute the inverse square root $\frac{1}{\sqrt{x}}$ , in other words $x^{- \frac{1}{2}}$ , we can take the logarithm, multiply it by $- \frac{1}{2}$ , and then take the exponent of the result. The log and exp floating-point functions are slow compared to just computing sqrt and dividing, so this normally wouldn't be a win, but what if we could get the log and exp conversion for nearly free? That's the trick behind the Q_sqrt function. Let's walk through it.

The first couple of statements bitcast the floating-point value number to an integer i:

	y  = number;
	i  = * ( long * ) &y;                       // evil floating point bit level hacking

Although the comment says it's doing some "evil floating point bit level hacking", all the function really does next with i is some basic arithmetic on the integer value before bitcasting it back to a float:

	i  = 0x5f3759df - ( i >> 1 );               // what the fuck? 
	y  = * ( float * ) &i;

If we ignore the "magic" number 0x5f3759df for a moment, then -(i >> 1) is just multiplying i by $- \frac{1}{2}$ , exactly what we would need to have done to the logarithm of number to get the logarithm of its inverse square root. Why does this work? A 32-bit int and a single-precision float both use the same number of bits in memory, but the int uses these bits to represent the integers in order, from $- 2^{31}$ to $2^{31} - 1$ , whereas a float on the other hand can represent both tiny fractional values as small as $2^{- 149}$ and larger than $2^{127}$ , because small float values are closer together than larger ones. In fact, they're distributed logarithmically. If we look at a graph of floating-point values mapped to their bit representations as integers:

graph of the bitcast float-to-int function

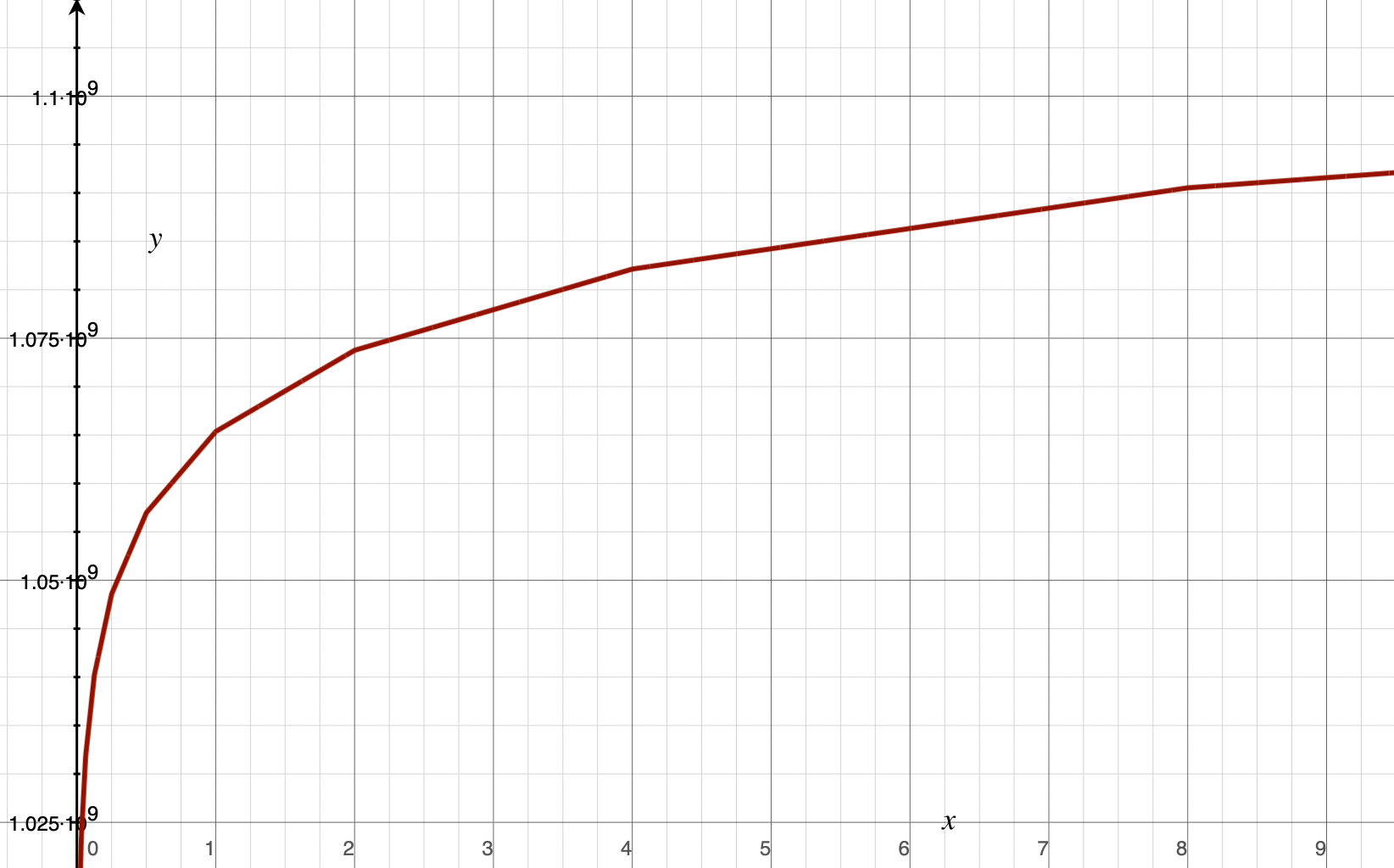
it's a spitting image for the logarithm function:

graph of the logarithm function

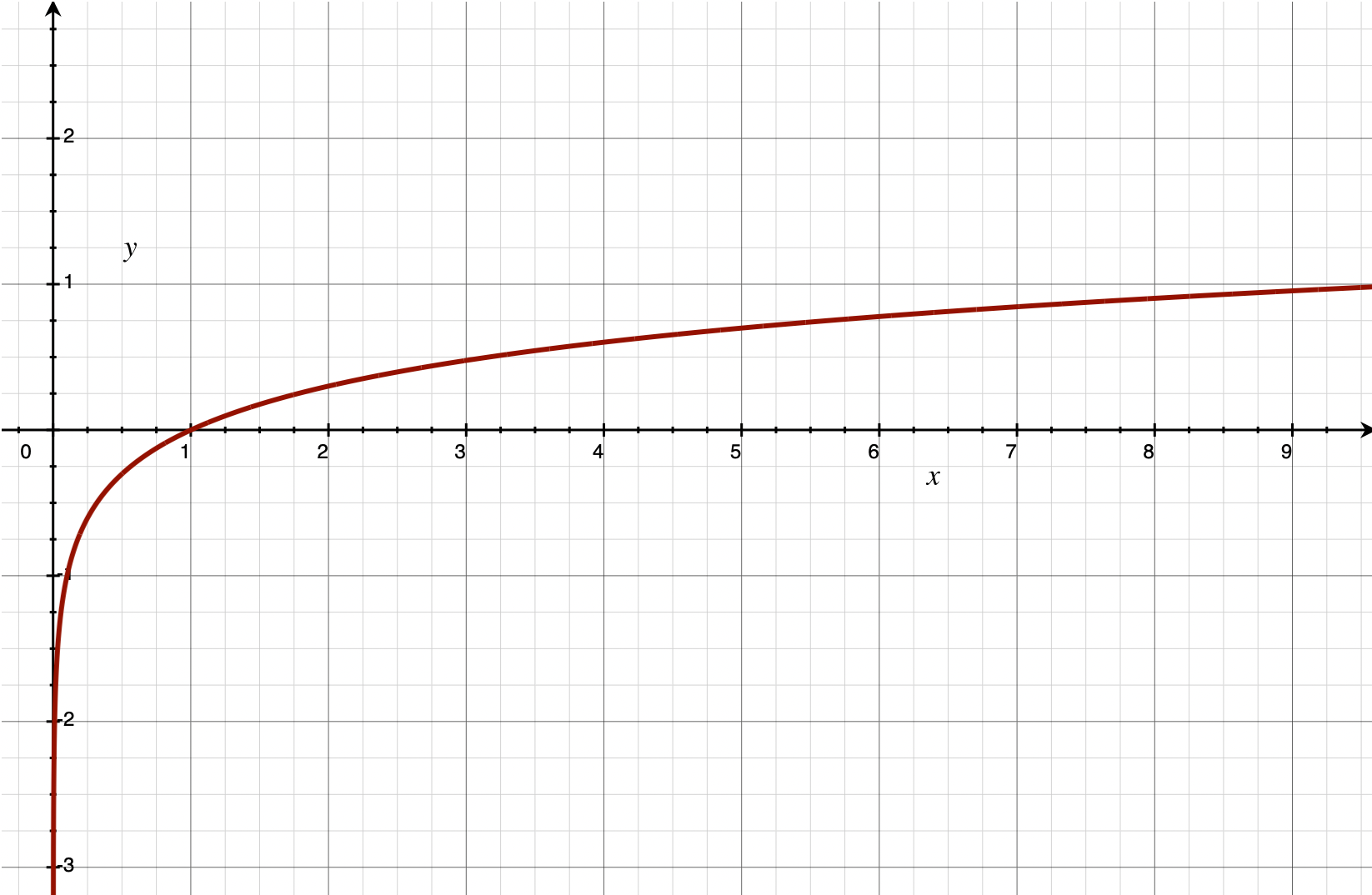
However, the curve for the bitcast function is "chunkier", with straight line segments between each power of two, and although the value of $\log 1$ for a typical logarithm function is always zero, the bit representation for the float 1.0 is a larger number. Nonetheless, it's still close enough that we can exploit the logarithm identities to get a decent approximation of the inverse square root. This is where the magic constant comes in—the bitcast operation is like taking the logarithm and adding a large bias value to it, giving approximately $\log x + K$ . Multiplying $\log x + K$ by $- \frac{1}{2}$ would give $\log \frac{1}{\sqrt{x}} - \frac{K}{2}$ . Before we bitcast back to float to invert the logarithm, we want the value of $\log \frac{1}{\sqrt{x}} + K$ , meaning we need to add $\frac{3 K}{2}$ . $\log 1$ is always zero, so the value of $K$ should be the floating-point bit representation of 1.0f, 0x3F80_0000. $\frac{3}{2}$ of that value is 0x5F40_0000, awfully close to the "magic" value 0x5F37_59DF, off by only 0x8A621. Adding the magic constant cancels out the bias, and the extra offset tries to minimize the distance between the two and improve accuracy of the result. (Modern numerical analysis has found that we can do even better than Carmack by adjusting the constant to 0x5F37_5A86 instead.)

The final stretch of the function uses Newton's method to improve the accuracy of the result before returning:

	y  = y * ( threehalfs - ( x2 * y * y ) );   // 1st iteration
//	y  = y * ( threehalfs - ( x2 * y * y ) );   // 2nd iteration, this can be removed

	return y;

Like the comment suggests, this can be repeated as desired to get the level of accuracy we want.

Let's refactor

The original Q_sqrt function is written in a very 90s style: abusing undefined behavior with pointer casting to do bitcasts, hardcoding magic constants, and doing other things to try to pre-optimize for a naive 90s compiler's limited optimization capability. Now that we understand how it works, we can write in a way that's both more technically correct according to the C standard and easier to understand while still getting good code generation out of a contemporary compiler. First, let's define some functions to do the bitcast conversion between int and float and back:

int float_to_bits(float x) {
  int result;
  memcpy(&result, &x, sizeof(int));
  return result;
}

float bits_to_float(int x) {
  float result;
  memcpy(&result, &x, sizeof(float));
  return result;
}

Then we can rewrite the function with a little less scary pointer stuff, and a little more explanation, as:

float Q_sqrt(float x) {
  // float_to_bits(x) for positive x is approximately log(x) + float_to_bits(1.0).
  // Shifting right and negating divides by -2, giving log(1/sqrt(x)) - float_to_bits(1.0)/2.
  // Adding float_to_bits(1.0)/2*3 gives log(1/sqrt(x)) + float_to_bits(1.0).
  int log_sqrt = -(float_to_bits(x) >> 1) + float_to_bits(1.0)/2*3;

  // Subtracting 0x8a621 improves the initial approximation slightly.
  // bits_to_float inverts the logarithm, giving the approximate 1/sqrt(x).
  float result = bits_to_float(log_sqrt - 0x8a621);

  // The inverse square root is the root of the function:
  //
  //   f(y) = 1/y^2 - x
  //
  // (that is, the value of y for which the function produces zero.)
  // The derivative of this function is:
  //
  //   f'(y) = -2/y^3
  //
  // If we have an estimate for the root, `y0`, then to use Newton's
  // method to improve the estimate, we do:
  //
  //   y1 = y0 - f(y0)/f'(y0)
  //
  // which in our case is:
  //
  //   y1 = y0 + (y0 - x*y0^3)/2
  //
  // or:
  //
  //   y1 = y0*((3/2) - (x/2)*y0^2)
  //
  // We can repeat this as many times as desired to converge toward the actual result.
  float x_half = 0.5f*x;
  result = result * (1.5f - x_half*result*result);
  // result = result * (1.5f - x_half*result*result);
  // result = result * (1.5f - x_half*result*result);

  return result;
}

You might be concerned that by adding these intermediate functions, and replacing the "magic" constants with elaborated equations, we'd be compromising the efficiency of the function, but contemporary optimizing compilers still constant-fold all of this away, and the added descriptiveness hopefully makes this version less mystifying to the next person who has to read it.

Limitations of this approach

So now we understand the "magic" behind this infamous function, and we can use the same technique to implement other mathematical operations. This is for fun only, though—aside from the code being nonobvious, there is little reason to actually do this sort of thing on contemporary CPUs. Quake III came out at a time when floating-point hardware had been standard issue for consumer hardware for only two-three CPU generations, and operations like division and square root were still relatively slow. Modern CPUs and GPUs can do pretty much any floating-point operation in a cycle or two, and even have dedicated inverse square root functions, and GPUs also support "half-precision" floats for occasions where the dynamic range of floating point is needed but accuracy isn't important.

That disclaimer aside, it's still OK to do things just for fun. So now let's imitate the inverse square root function's technique to define another math function.

"Fast" reciprocal

Division is another traditionally slow operation for older floating-point units, so let's make a "fast" reciprocal. The logarithm of a number's reciprocal is the negative logarithm of the original number, $\log \frac{1}{a} = - \log a$ . Bitcasting float to int approximates $\log a + K$ , and negating that gives $- \log a - K$ , so we need to add $2 K$ in order to get the approximation of $- \log a + K$ we're looking for. So our first approximation looks something like this:

float Q_recip(float x) {
  // float_to_bits(x) for positive x is approximately log(x) + float_to_bits(1.0).
  // -float_to_bits(x) is thus approximately log(1/x) - float_to_bits(1.0).
  // Adding 2*float_to_bits(1.0f) gives log(1/x) + float_to_bits(1.0).
  // bits_to_float inverts the logarithm, giving approximately 1/x.
  float result = bits_to_float(
    -float_to_bits(x) + 2*float_to_bits(1.0f));

  return result;
}

And let's see how it works with a few test cases:

void test(float x) {
  printf(u8"1/%f = %f ≈ %f\n", x, 1.0f/x, Q_recip(x));
}

int main() {
  test(1.0f);
  test(2.0f);
  test(3.0f);
  test(4.0f);
  test(5.0f);
}

which prints:

1/1.000000 = 1.000000 ≈ 1.000000
1/2.000000 = 0.500000 ≈ 0.500000
1/3.000000 = 0.333333 ≈ 0.375000
1/4.000000 = 0.250000 ≈ 0.250000
1/5.000000 = 0.200000 ≈ 0.218750

It's not a great approximation for non-power-of-two inputs, but it's in the ballpark. As with the Q_sqrt function, we can use Newton's method to improve the approximation further:

float Q_recip(float x) {
  // float_to_bits(x) for positive x is approximately log(x) + float_to_bits(1.0).
  // -float_to_bits(x) is thus approximately log(1/x) - float_to_bits(1.0).
  // Adding 2*float_to_bits(1.0f) gives log(1/x) + float_to_bits(1.0).
  // bits_to_float inverts the logarithm, giving approximately 1/x.
  float result = bits_to_float(
    -float_to_bits(x) + 0x7f000000);

  // The reciprocal of `x` is the root of the function:
  //
  //   f(y) = x - 1/y
  //
  // (that is, the value of y for which the function produces zero.)
  // The derivative of this function is:
  //
  //   f'(y) = 1/y^2
  //
  // If we have an estimate for the root, `y0`, then to use Newton's
  // method to improve the estimate, we do:
  //
  //   y1 = y0 - f(y0)/f'(y0)
  //
  // which in our case is:
  //
  //   y1 = y0 - (x - 1/y0) * y0^2
  //
  // or:
  //
  //   y1 = (2 - x*y0)*y0
  //
  // We can repeat this as many times as desired to converge toward the actual result.

  result = (2.0f - x*result)*result;
  // result = (2.0f - x*result)*result;
  // result = (2.0f - x*result)*result;

  return result;
}

which gives:

1/1.000000 = 1.000000 ≈ 1.000000
1/2.000000 = 0.500000 ≈ 0.500000
1/3.000000 = 0.333333 ≈ 0.328125
1/4.000000 = 0.250000 ≈ 0.250000
1/5.000000 = 0.200000 ≈ 0.198242

which is quite a bit closer. We can uncomment one of the other iterations:

1/1.000000 = 1.000000 ≈ 1.000000
1/2.000000 = 0.500000 ≈ 0.500000
1/3.000000 = 0.333333 ≈ 0.333252
1/4.000000 = 0.250000 ≈ 0.250000
1/5.000000 = 0.200000 ≈ 0.199985

which is good to three digits or so, not bad!

Other functions to try

Now that you've seen the overall technique, here are some other fun functions to try to implement:

the regular square root,
cube root, and inverse cube root,
natural logarithm and exponent

Many things in software that appear to be "magic" can really be understood by anyone. Hopefully this post helped take the magic away from this infamous bit of code for you.